CODEFORCES ROUND #278 Div.2 PROBLEM A : GIGA TOWER

Problem Link : http://codeforces.com/contest/488/problem/A

We just need to make an function of finding whether a number has a digit 8 or not.....  &

For -9<x<0     answer will be 8-x

For x>=0       iterate up from x till the answer

For x<-8       iterate  down from abs(x) till the answer

Sample Test Cases:

                           Answer

-192                       3/-189

192                        6/198

-7                         15/8

 Don't forget to take number as long integer :P

CODEFORCES ROUND # 277.5 Div2 C. Given Length and Sum of Digits...

Problem Link: http://codeforces.com/problemset/problem/489/C

Death Call Problem!!! :P

If number has length of m and having sum as S
then minimum amd maximum nos. could be found out by ::

Set MAXNO[m]= 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0...................
Set MINNO[m]=1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0...........

Increment the nos. in MAXNO from left till 9 and jump to its right till we get the required sum S
 Similarly ,
Increment the nos. in MINNO from right till 9 and jump to its left till we get the required sum S

These are our required results!!!!!!11

Dont miss the testcase: 1 0
Expected Output: 0 0

Code Link:  http://pastebin.com/eujy24nt

MINIMUM DISTANCE BETWEEN NODES IN TREE

Distance b/w two nodes in tree such as:

                                                              1
                                     2                                                  3
                      4                        5                           6                            7
             8             9          10          11           12           13         14           15

Ex.: 
 Distance b/w nodes 8 and 15 =>>6   
        ( 8->4->2->1->3->7->15)    6 vertices

 Distance b/w nodes 8 and 10=>>3

     while(i!=j)
     {
                if(i>j)
                     {
                        i=i/2;
                         count++;
                      }
                else
                    {
                       j=j/2;
                       count++;
                    }
      }

where i is intial node and j is final node :)

SPOJ PROBLEM 3921: THE GREAT BALL (BYTESE2)

Selection Process :)
Code:

#include<vector>
#include<iostream>
#include<algorithm>
using namespace std;

int main() {
    int t;
    cin>>t;
    while(t--)
    {
        vector< pair<int,int> > v;
        int n;
        cin>>n;
        for(int i=0;i<n;i++)
        {
            int a,b;
            cin>>a>>b;
            v.push_back(make_pair(a,b));
        }
        /*for(int i=0;i<v.size();i++)
        {
        cout<<v[i].first<<" "<<v[i].second<<endl;
        }*/
        sort(v.begin(),v.end());
        int max=0;
      for(int j=0;j<v.size();j++)
      {
        int count=1;
        for(int k=0;k<v.size();k++)
        {
        if(k==j)  continue;
        if(v[k].first<v[j].second && v[k].second>=v[j].second)
              { count++;
               //cout<<"h"<<endl;
               }
        }
        if(count>=max)
          max=count;
        }
        cout<<max<<endl;
    }
    // your code goes here
    return 0;
}

YET ANOTHER PROBLEM BASED ON SIEVE OF ERASTOTHENES

Problem Link: http://www.spoj.com/problems/ETF/

Euler’s totient function:

The number of positive integers, not greater than n, and relatively prime with n, equals to Euler’s totient function φ (n). In symbols we can state that
φ (n) ={a Î N: 1 ≤ a ≤ n, gcd(a, n) = 1}
This function has the following properties:

1. If p is prime, then φ (p) = p – 1 and φ (p^a) = p a * (1 – 1/p) for any a.
2. If m and n are coprime, then φ (m * n) = φ (m) * φ (n).
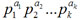3. If n = , then Euler function can be found using formula:

φ (n) = n * (1 – 1/p1) * (1 – 1/p2) * ... * (1 – 1/pk) 

For more http://en.wikipedia.org/wiki/Euler%27s_totient_function

Modify sieve as: all the multiples of prime nos. would have prime no. as divisor. So, just modifying it there only would produce the desired result.

Euler Function:

void sieve()
{
    prime[0]=0;
    prime[1]=1;
    for(long long i=2;i<MAX;i++)
    {
        if(!prime[i])
            {
             prime[i]=i-1;//For prime nos. euler(i)=i-1  Property 1
                
                for(long long j=2*i;j<MAX;j=j+i)
                {
                    if(!prime[j]) 
                           prime[j]=j; //First visit to the no.
                    prime[j]=prime[j]/i*(i-1); 
     //it couldn't be written as prime[j]*(i-1)/i as it gives 0 :P                }
            }
    }
}

But it gives TLE .Still some more modifications are needed up :)


 

SIEVE OF ERASTOTHENES BASED SPOJ PROBLEMS

PROBLEM LINK:
http://www.spoj.com/problems/PRIME1/
http://www.spoj.com/problems/APS/
http://www.spoj.com/problems/AFS/

Approach is pretty same for all three problems.
Precomputation is needed .
Common approach to problems is initialize them initially to 0 or 1 as per ur choice and sieve it out.

Problem 1: http://www.spoj.com/problems/PRIME1/

Take an array
Mark all the multiples of no. by 1 or 0 
Pseudo Approach::
       1 2 3 4 5 6 7 8 9 10
a[n]   0 0 0 0 0 0 0 0 0 0    ==>>intial
       0 0 0 1 0 1 0 1 1 1    ==>>final
Prime nos.: 2 3 5 7  (marked with 0s)

Problem 2:http://www.spoj.com/problems/APS/

Take two arrays i.e. one for f(n) and the other for a[n]
pre-compute f(n)
marks all multiples of no. with the no.   ex.:  a[2]=2  a[4]=2  a[6]=2  a[8]=2...........................
Pseudo Approach::
           1 2 3 4 5 6 7 8 9 10
  f(n)     0 0 0 0 0 0 0 0 0 0      ==>>initial 
           0 2 3 2 5 2 7 2 3 2      ==>>final
  a[n]     0 0 0 0 0 0 0 0 0 0      ==>>initial
           0 2 5 7 12 14 21..................... ==>> final  

Problem 3:http://www.spoj.com/problems/AFS/ 

Take one array 
pre-compute the sum
add the no. to the multiple of the no.   ex.:     a[2]=1    a[4]=a[4]+2   a[6]=a[6]+2........................
Pseudo Approach::
         1   2    3    4    5   6   7   8   9
f(n)     0   0    0    0    0   0   0   0   0  ==>> initial
         0   1    1    3    1   6   1   7   4  ==>>final
a[n]     0   0    0    0    0   0   0   0   0
         0   1    2    5    6   12  13  20  24..

:) :)

C# SOLUTION TO SPOJ PROBLEM 1:TEST

Problem Link : Life, the Universe, and Everything

Code:

using System;
public class Test
{
    public static void Main()
    {
        int a=0;
        a=int.Parse(Console.ReadLine());
        while(a!=42)
        {
            Console.WriteLine(a);
            a=int.Parse(Console.ReadLine());
        }
        // your code goes here
    }
}