YET ANOTHER PROBLEM BASED ON SIEVE OF ERASTOTHENES

Problem Link: http://www.spoj.com/problems/ETF/

Euler’s totient function:

The number of positive integers, not greater than n, and relatively prime with n, equals to Euler’s totient function φ (n). In symbols we can state that
φ (n) ={a Î N: 1 ≤ a ≤ n, gcd(a, n) = 1}
This function has the following properties:

1. If p is prime, then φ (p) = p – 1 and φ (p^a) = p a * (1 – 1/p) for any a.
2. If m and n are coprime, then φ (m * n) = φ (m) * φ (n).
3. If n = 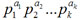, then Euler function can be found using formula:

φ (n) = n * (1 – 1/p1) * (1 – 1/p2) * ... * (1 – 1/pk) 

For more http://en.wikipedia.org/wiki/Euler%27s_totient_function

Modify sieve as: all the multiples of prime nos. would have prime no. as divisor. So, just modifying it there only would produce the desired result.

Euler Function:

void sieve()
{
    prime[0]=0;
    prime[1]=1;
    for(long long i=2;i<MAX;i++)
    {
        if(!prime[i])
            {
             prime[i]=i-1;//For prime nos. euler(i)=i-1  Property 1
                
                for(long long j=2*i;j<MAX;j=j+i)
                {
                    if(!prime[j]) 
                           prime[j]=j; //First visit to the no.
                    prime[j]=prime[j]/i*(i-1); 
     //it couldn't be written as prime[j]*(i-1)/i as it gives 0 :P                }
            }
    }
}

But it gives TLE .Still some more modifications are needed up :)